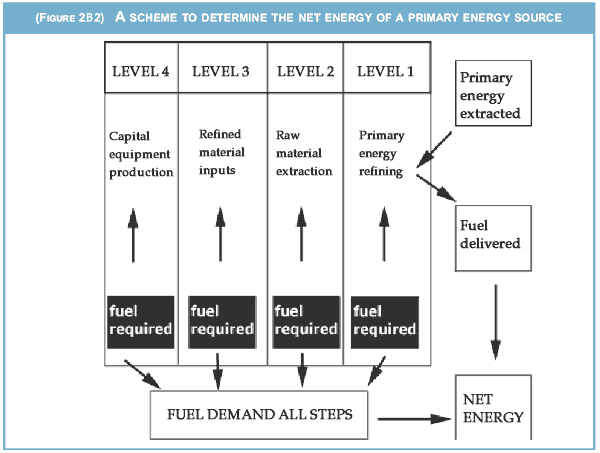
The objective of a net energy calculation is to determine the overall amount of primary energy dissipated in order to bring one unit of fuel into use. The result will vary with the energy type, the degree of depletion of the source, and the nature of the deposit. It will also vary with time and technology. The approach is a uniquely valuable concept in economic analysis, payback time estimation, life cycle analysis and the efficient allocation of capital resources between competing energy technology systems. It is also a very simple concept, though certain procedures have to be taken if the results of analysis are to be meaningful. The most important of these is system boundary: this has to be fixed to ensure that everything is taken account of from the moment a primary resource leaves the ground (or wherever) to its delivery to the market as a directly usable fuel.
DOING THE SUMS
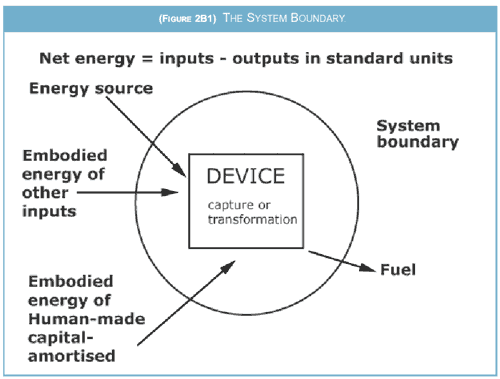
The first step in calculating net energy is to determine what are all the inputs, other than labour and management, that are drawn in when a primary energy source is extracted and transformed into a marketable fuel or fuels. If there is capital stock involved, as must almost certainly be the case, then its embodied energy, amortised, must be included. If there are material inputs, their embodied energy must also be counted. Figure 2B1 offers a scheme for this analysis.
 It is clearly advantageous to have an agreed set
of conventions for such calculations so that
numbers can be compared, and conclusions
reliably drawn. In 1974, following the first
OPEC oil price hike, there was a flurry of energy
analysis calculations ranging from the energy
to produce a loaf of bread to the production
of a kWh of electricity via a nuclear reactor.
The chaos of methods at that time, not dissimilar
from the disparity of corporate accounting
conventions today, called for action. The
International Federation of Institutes of
Advanced Study (IFIAS), which was launched
in the aftermath of the Stockholm Environment
Conference in 1972, asked me to pull together a
group to work out an appropriate set of conventions.
I was given carte blanche to travel round
the world to find appropriate activists. The
group that met in Guldmedhytten, Sweden, in
1974 comprised economists, engineers, system
analysts, chemists, physicists, academics and
corporate managers. In one week of resolute
discussion they produced a set of conventions
summarised in the booklet called 'Energy
Analysis, IFIAS Report 6'. Amazingly there
was a 100% consensus.
It is clearly advantageous to have an agreed set
of conventions for such calculations so that
numbers can be compared, and conclusions
reliably drawn. In 1974, following the first
OPEC oil price hike, there was a flurry of energy
analysis calculations ranging from the energy
to produce a loaf of bread to the production
of a kWh of electricity via a nuclear reactor.
The chaos of methods at that time, not dissimilar
from the disparity of corporate accounting
conventions today, called for action. The
International Federation of Institutes of
Advanced Study (IFIAS), which was launched
in the aftermath of the Stockholm Environment
Conference in 1972, asked me to pull together a
group to work out an appropriate set of conventions.
I was given carte blanche to travel round
the world to find appropriate activists. The
group that met in Guldmedhytten, Sweden, in
1974 comprised economists, engineers, system
analysts, chemists, physicists, academics and
corporate managers. In one week of resolute
discussion they produced a set of conventions
summarised in the booklet called 'Energy
Analysis, IFIAS Report 6'. Amazingly there
was a 100% consensus.
Unfortunately this book was not given an ISBN number and with the demise of IFIAS is now unavailable. I am told it can be obtained from the British Library, Boston Spa. However an adequate summary is given in chapter 12 of my 1978 publication Energy in the Economy.1 A less detailed but wider ranging exposition, also published in 1978, is still available from the International Institute for Applied Systems Analysis.2
The IFIAS convention defined two important units of account:
GROSS ENERGY REQUIREMENT (GER)
(I quote) 'The gross enthalpy of combustion released at standard state of all the naturally occurring energy sources which must be consumed in order to make a good or service available'. The standard state is the one frequently adopted in physico-chemical texts, namely 0ºC and 1 bar pressure.
ENERGY REQUIREMENT FOR ENERGY
If one now subtracts from this GER the available enthalpy in the fuel delivered, the difference is the net energy. IFIAS called this the Energy Requirement for Energy, ERE.
ERE = GER per unit enthalpy of delivered fuel.
Note the use of the word 'requirement'. One often hears the use of the word 'energy cost' used in the sense of the amount of energy embodied or used to in producing something. This could also imply monetary cost, hence the strict use of the world 'requirement' in the IFIAS conventions.
Another convention well worth following is to
use distinct numeraires for electricity and heat
(enthalpy). Thus watt-hours or a multiple thereof
for electricity (which has high thermodynamic
potential), and an enthalpic unit for heat,
such as Mega-joule (MJ), Giga-joule (GJ),
Tonnes oil equivalent (TOE) or even barrels (of
oil). Unfortunately several statistical sources,
such as in the UK, have chosen to use watthours
as representing heat units. So if using
such sources beware.
It may be seen that with such a definition ERE is always greater than unity, and the larger the value the poorer the yield and the more energy that is dissipated in converting it into a fuel useable by the market. For example the ERE of North Sea oil is in the region of 1.03, whereas tar sands in Canada are closer to 1.15. An important criterion, often overlooked, is the area requirement, that is the net energy per unit area. This is a particularly important criterion when evaluating biomass-to-energy proposals, such as alcohol from maize, or heat from wood fuel.
Working out the numbers for any particular fuel type and source is complicated by the fact that it almost always invokes a contribution of electricity. Now 1 kWh of electricity has, by definition, a heating value if 3.6 MJ. However creating this from some heat source will require between 2.5 and 3.5 times 3.6 MJ, according the fuel type and technology transformation. This is because electricity has a very high thermodynamic work potential. The potential efficiency of conversion of heat to work may be determined through the Carnot equation3 .
The fuel used will also have gone through some extraction and purification processes. The upshot, for the case of the UK is that to deliver 1 kWh to a commercial user in the UK in year 2002 dissipates 14.3 MJ primary energy per kWh delivered.
Two conceptual problems arise when the electricity source is from nuclear energy or renewables. Some international statistics attribute to electricity a value of 3.6 MJ/kWh, while others attribute the heat dissipated in the transition. This latter is the more accurate representation, but not perfect since, for example, not all nuclear fuel is burnt. It is a reminder to us all that energy statistics are far from precise and are affected by a number of questionable conventions.
In the case of renewables, except for the energy embodied in the structure (of, say, a wind or wave turbine), there is no fuel requirement. In my view it is correct to take the primary energy content of the delivered electricity as being the fossil energy embodied in manufacturing and the delivering the turbine to site and its subsequent maintenance. With this convention the primary energy of wind turbine electricity in the UK today may be said to be around 0.2 MJ/kWh.
HEAT AND WORK
It is not heat that drives the economy, but thermodynamic work. In the UK about 55% of all heat is converted to thermodynamic work, often at very low efficiency as in a petrol engine. Strictly speaking all energy analyses ought to be conducted in these terms, but the data requirements are formidable. Indeed there is only one now famous example of this being done, that of Berry and Fels.4 The alternative, advised by the IFIAS group, is to express GER and ERE in terms of energy sources of a standard quality - the definition of this being the extent to which the heat of combustion could be turned into work. As it happens hard coal, natural gas and hydrocarbons have values within 2% of each other, and since no analysis can be that accurate, this is the adopted standard. Note that wood fuel and alcohol fuels have considerably lower potentials. Electricity has almost 100% availability as work.
MODELS
These calculations are made vastly easier if there is at hand an energy numeraire (i.e. Natural Capital Accounting/ ECCO) model of the economy. Such models are constructed to determine the elements of each conversion and then to assemble them as an overall system average. This average value will change as the energy mix changes through time.
Thus a fairly accurate value can be determined at any moment in time for the average amount of primary energy dissipated to deliver one unit of marketable heat to the market. In the ECCO model framework this is known as SYSGER - System GER (GJ in per GJ delivered). Such models also deliver another useful average, FEREL: the average fuel energy required to deliver one unit of electricity (GJ per kWh). This can be taken back to primary energy by multiplying FEREL by SYSGER to get GEREL - the average primary energy input to produce one kWh of electricity, which as remarked above is about 14.3 for the UK in 2002.
Such models exists for the UK, Scotland and many other countries. David Crane and Larry Staudt have developed an ECCO model for Ireland that is described in this book.
RENEWABLE ENERGY SOURCES
The application of the above principles to renewable energy sources is simple. The inputs are human-made capital, that is to say output of the manufacturing system, its delivery to site and erection and its expected lifetime maintenance and the infrastructure of delivery. This input can then be set against the output expected over its anticipated lifetime. Since most renewable systems deliver electricity how does one measure the net energy? Well, let us suppose that a particular wind farm cost £700,000 per MW capacity (1.05 million Euros). Using UK data, from the UK ECCO model we know that the energy intensity of human-made capital in a given year was (18MJ/£). Hence an approximate value for the energy embodied in the turbines, etc. will be 12,600 GJ. Let us add another 20% for lifetime maintenance, making 15,000 GJ over its lifetime of, say, 30 years.
The potential yield from a one MW turbine is 8760 MWh/year (8760 hours in a year) or 283 thousand kWh over 30 years. However the wind does not always blow. UK averages are about 28% (load factor 0.28) of this potential. Thus the yield over its lifetime is about 75 million kWh. That makes the energy embodied about 0.2 MJ/kWh.
Taking UK figures, as remarked above, the GEREL for the UK is 14.3 MJ/kWh. Hence had these 75 million kWh been generated from fossil or nuclear sources, the equivalent of 1.05 million GJ of primary energy would have been required. The initial energy investment, therefore is returned within 15,000/1,005,000 = 0.43 of a year or 5 months.
From this data set it is easy to calculate how much carbon dioxide will be reduced. If one has an ECCO model this data will be generated automatically
Note, however, that as the fossil or nuclear sector becomes more thermodynamically efficient, or as renewables penetrate, the relative advantages will diminish. That is, the payback time will increase. Eventually with a 100% renewable electricity there is potential for, as it were, energy breeding.
There are other renewable energy systems such as photo-voltaics where the pay-back times are not so favourable. The energy embodied in these devices depends on the type of cells. There are highly efficient cells used in space satellites, whose net energy is certainly negative, but in such a situation this is not the important criterion. However for terrestial uses, there is no point in a negative net energy system. It would be like a farmer having to use all his crop to plant next year's crop and have to buy in more seed as well. The energy embodied in photo-voltaic cells is certainly falling. A recent figure quoted in then literature was 100,000 GJ/MW. Such cells tend to have lower load factor than wind turbine. 13% is often quoted. On this basis the pay-back time would be about 6 years.
ENERGY STORAGE
The Achilles heel of renewable-generated electricity is the variable output and low load factor, which means that if there were ever to be a high degree of replacement of conventional means of generation, some means of storage are needed. Two obvious ones spring to mind: pumped storage and conversion of electricity of hydrogen by electrolysis of water, a well developed technology. It takes 385 kWh to create one GJ of hydrogen, but at low voltage. As a renewable based economy develops one assumes that it will become more and more electrically driven, but storage will remain expensive in net energy terms. The single greatest problem will be in transport fuels, where fuels cells will be the dominant device using methanol or hydrogen. The key thing to look at here is that the supply train will now be reversed. Instead as now, of a flow from primary energy to fuels to electricity, we shall have electricity to hydrogen to fuel cells.
EXAMPLE
The transition to a renewable-based economy is not going to easy or cheap. We shall need all the oil and gas we can get to fuel it. A recent study I helped to carry out for the European Commission6 showed that for the European Union to switch to a renewable energy economy was not going to easy, especially if we expect to hold on to what seems to me to be three entrenched criteria:
- that unemployment should be kept low
- that self-sufficiency in energy should be main tained or raised.
- that material welfare should grow annually
In fact the study, which used an ECCO model of the European-15 showed that all three criteria could not be met simultaneously.
Compromises on material welfare - the growth rate - were inevitable. In fact the three targets set for us by the European Commission were to
- Achieve an acceptable level of unemploy ment.
- Meet the 1997 Kyoto international protocol commitments on carbon dioxide emissions.
- Increase the European Union's self-sufficiency in energy supply.
Each of these targets requires a set of policies to achieve it. According to conventional thinking the policies might be as follows:
- To reduce unemployment: further expansion of the economy by borrowing externally.
- To reduce carbon dioxide: massive investment in energy conservation.
- To increase self-sufficiency in energy: major investment in renewable energy systems for electricity generation.
To avoid burdening the reader with a torrent of results, the effectiveness of each set of policies in attaining its aims was judged by comparing it with a benchmark called business-as-usual (BAU). Here we assumed that all current policies and trends in the European Union continued unchanged over the next fifteen years to 2015.
Of course, such an unchanging evolution of the economy will not happen. As events unfold, new initiatives, new technologies and new options will be grasped. However it is useful to be informed of what might happen if nothing is done because then politicians can take time by the forelock and obviate some of pitfalls lying ahead!
Here is the business-as-usual (BAU) outcome for the European Union's current fifteen countries (EU-15) for the year 2015 compared to 1999:
- Economic growth is about 2% annually.
- Manufacturing output is up 50%.
- The material standard of living is up 20%.
- Primary energy demand is up 50%.
- Carbon dioxide output is up 45%.
- Self-sufficiency in energy falls to 25%.
- Unemployment is very high, maybe even 30%.
If we adopt Keynesian policies and borrow to make the economy expand faster to reduce unemployment, we calculated the results in 2015 would be:
- Growth rate: 40% higher than BAU.
- Manufacturing output: 90% greater than BAU.
- Material standard of living: 70% higher than BAU.
- Primary energy demand: 45% higher than BAU.
- Carbon dioxide output: 60% higher than BAU.
- Unemployment falls to 4%.
However the cost of all this was a huge rise in EU-15 external debt. Moreover the employment objective was met at the expense of reduced environmental and physical sustainability. We concluded that non-indigenous growth was not a sustainable path, nor the right way to reduce unemployment.
What happens if we concentrate on cutting carbon dioxide emissions by massive investment in energy efficiency measures? Here is the outcome by 2015.
- Growth rate: much the same as BAU.
- Manufacturing output: about the same as BAU.
- Material standard of living: 15% less than BAU, i.e. practically no rise at all from the year 2000.
- Primary energy demand: 30% lower than BAU.
- Carbon dioxide: meets the Kyoto commit ment.
- Unemployment: much the same as BAU - unacceptably high.
In short, this strategy shows a huge improvement in output per unit energy use and a significant reduction in carbon dioxide, meeting EU commitments. However it does nothing for the curse of unemployment and the material standard of living falls.
So what happens then if we make greater energy self-sufficiency the priority since, in both tests described so far, the EU-15 became increasingly dependent on fuel imports even with a major effort towards conservation? Could a fast track investment programme in renewable energies improve matters? To investigate, we assumed a deliberate government-led programme of investment in renewable energy systems: a mix of wind turbine and photovoltaic. Such a policy would be considered wildly uneconomic, at least in the early stages. We assumed too that the resulting growth in renewables would be accompanied by a learning curve resulting in an eventual halving of the amount of human-made capital required per unit of power over the trial period. This was the outcome by 2015:
- Growth rate: 45% less than BAU.
- Manufacturing output: 25% more than for the year 2000, but 11% less than BAU.
- Material standard of living: 24% down on BAU.
- Primary energy: demand 20% less than BAU
- Self-sufficiency in energy: better than BAU with 33% of electricity from renewable sources.
- Unemployment: even higher than BAU.
So, although self-sufficiency in energy was improved, the other outcomes made this an unattractive policy. The reduced output and increased unemployment were directly due to the massive diversion of capital to investment in renewables which, because of their low load factors, require about three times as much investment per unit output as conventional or nuclear energy sources.
What was clear from these trials is that though it is possible to solve one problem, all three cannot simultaneously be solved. This is an important insight and leads to a search for a set of policies that better meets one's aims.
CONCLUSION
A renewable-based economy is certainly possible so far as the supply side - nature - is concerned. The investment requirements are going to be formidable - greater than with nuclear power. The transition will take time and require the embodiment of much energy. To make this transition we shall need all the fossil fuels we can get. And the sooner we start the easier it will be. We certainly will have to start before it becomes 'economic' using that word in its traditional sense. This is where examining new energy proposals in the light of net energy are immensely valuable.
REFERENCES
1. Slesser, M, (1978), Energy in the Economy, Macmillan, London, ISBN 0-333-21495; chapter 12 This is one of almost 50
chapters and articles in the 336-page large format book, Before the Wells
Run Dry. Copies of the book are available for £9.95 from Green Books.
2. Slesser, M (1978), Energy Analysis: its utility and limits, RM-78-46, IIASA, 2361, Laxenburg, Austria
3. The Carnot equation states that the maximum fraction of a quantity of heat that can be turned into work (in
the thermodynamic sense) is given the ratio (temperature of the heat source - temperature of surroundings (sink)) / temp of heat source, in units of absolute temperature. Thus 100% efficiency of conversion is
unattainable.
4. Berry, S & Fels, M (1973), 'the energy cost of automobiles', Science and Public Affairs, Dec. issue.
5. That is Gibbs Free Energy. These data were published by the American Physical Society in 1974
6. Modelling a socially and environmentally sustainable Europe, Contract SOE1-CT96-1018, under the
Targeted socio-economic research programme (TSER), technical report published by the Wuppertal Institute,
Germany, 1998. In this study the European Union 15 countries are treated as a single entity.
